ChatGPT: Total game-changer, still no I in AI

After recently giving ChatGPT a shot, I was keen to try putting it through its paces to see how smart it actually is. Could it really replace a developer? So when I came across a problem I wanted to solve that would involve writing an algorithm, I saw my opportunity.

Background

Thanks to a recommendation from my sister, I got hooked on a new puzzle game. It’s called 4=10 (Android / iOS) and the name pretty much says it all. You are given 4 numbers and you need to make them equal 10. You can use the operators any number of times, except the parentheses which you can only use once. Some levels disable certain operators to make things a bit tricker. A pretty simple premise, but very addicting.

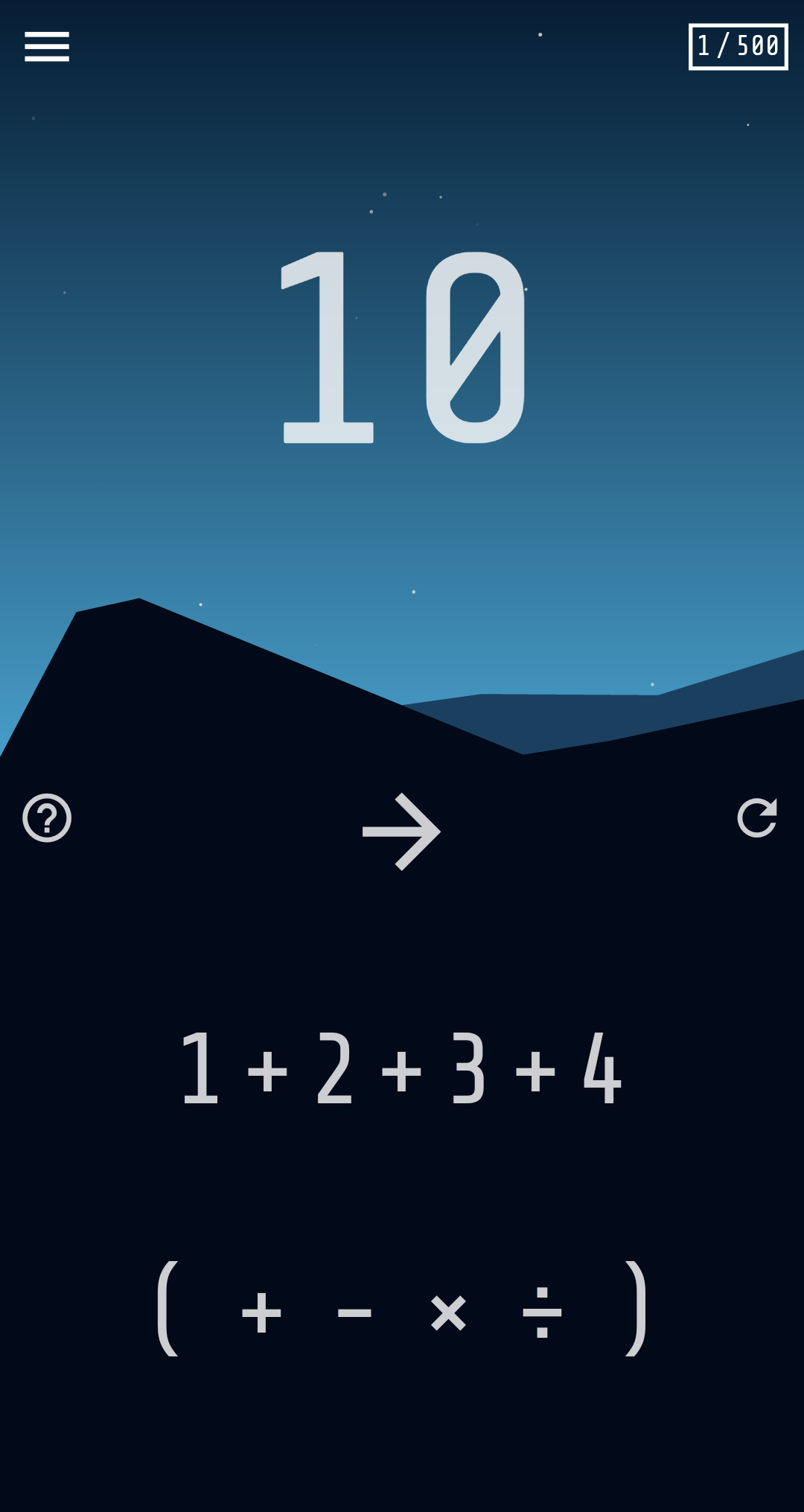
For instance:

Could be solved with:

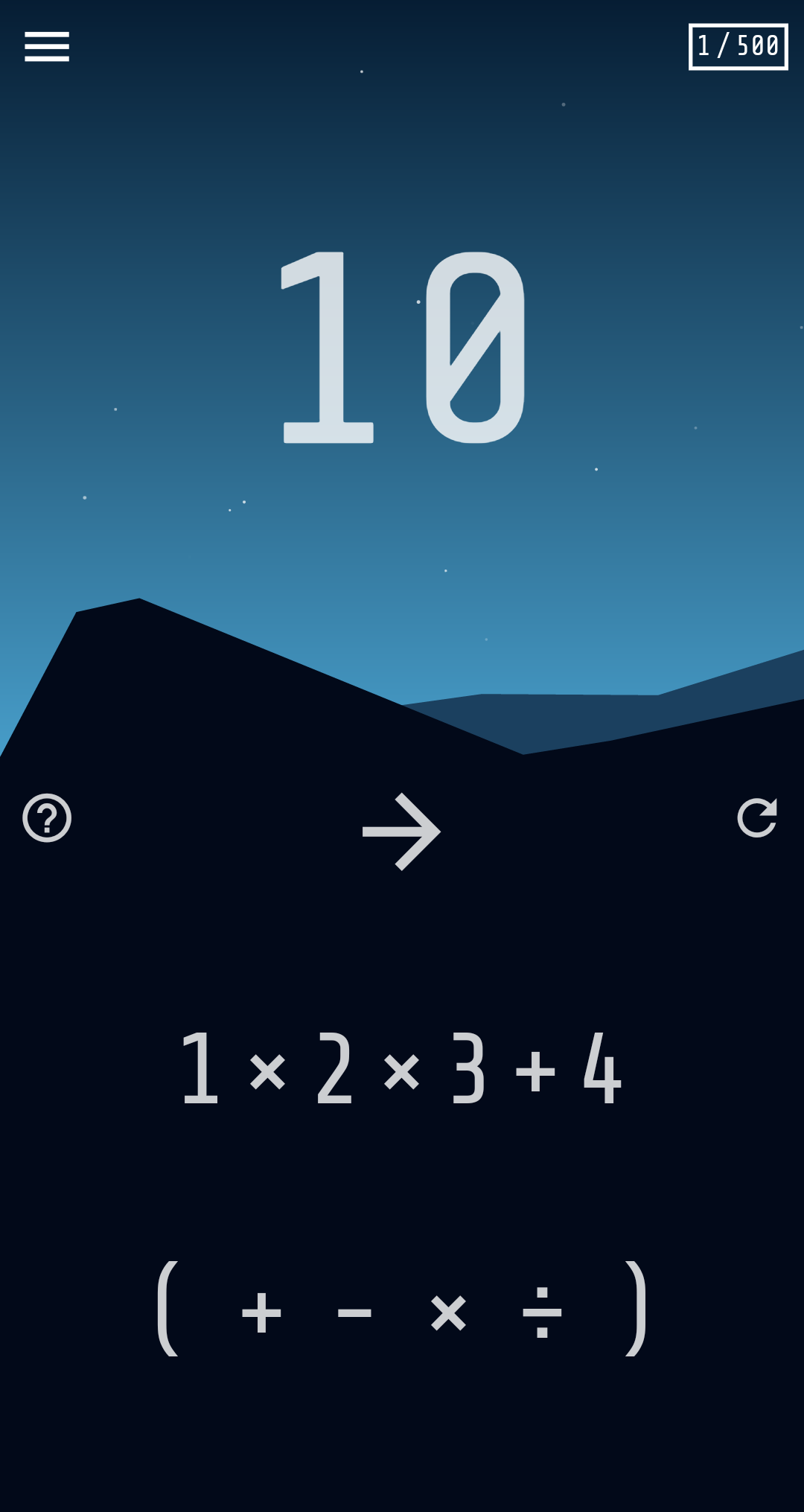
Or:

I was absolutely blazing through these. Every now and then I would come across a real head-scratcher, but the solution usually materialized pretty quickly after trying a few different combinations. That is, until I got to this one:

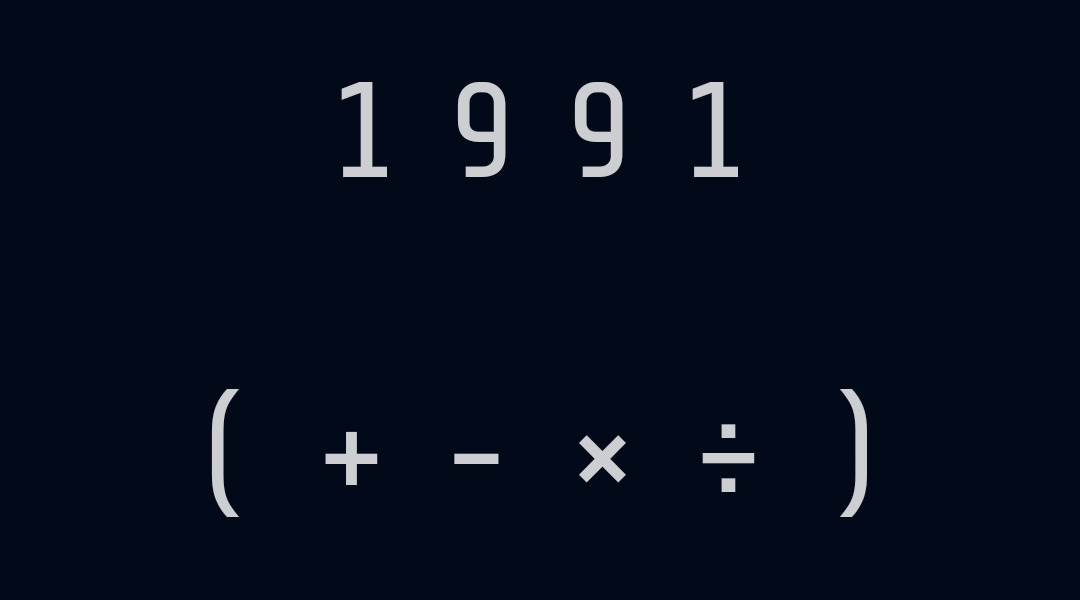
I was stumped.

I spent so long on the damn thing, I would have sworn I tried every possible iteration. For the first time, I tried to use one of the hints. That’s when I realized, they don’t actually have any hints. It just gives you the solution! I wasn’t ready for complete surrender, I was just hoping for a bit of a nudge in the right direction. So what now?

Well, if I could somehow calculate all the possible solutions, I could filter through the list of solutions to provide some helpful hints. How many unique solutions are there? Is it possible without parentheses? Perhaps I could display just the operations for a solution, or just the order of numbers. Are there operators that are never used? Are there operators that are used in every solution?

Easy enough, I just need to write a program to find all possible equations for any given 4 digits that equal 10.

ChatGPT to the rescue?

I thought of some of the basic concepts I would have to take into consideration to create the algorithm. The order of operations and mathematical properties (associative, commutative) will determine whether equations are functionally identical — just rearranged. For instance: 1+2+3+4 is the same as 4+3+2+1. Similarly, (3*4)/2+4 is the same as 4+3*4/2. So I don’t want to find all the solutions, just the mathemathically unique ones.

Now I have a good idea of what my input will be, what I expect as output and some general concepts to help produce the desired output.

This seemed like a good place to start with a ChatGPT prompt. My first prompt contained a lot of detail: what the algorithm would need to do, how the input and output will be formatted, what considerations to make, the requirements for which operations can be used, etc.

The reply it gave me was impressive, but certainly not an algorithm. Instead, it did what it does best — explained how I could write such an algorithm.

And to its credit, it did have some good ideas. Here are some highlights from its initial response:

You can use the itertools library in python to generate all possible permutations of the 4 numbers, and recursively add the different mathematical operations and parenthesis. To avoid calculating duplicate solutions, you can use a set data structure to store the unique solutions and check if a solution has already been found before adding it to the set.

It pointed me towards itertools, definitely a useful library for this project. It also recognizes that duplicate solutions will be generated and that common data structure would be required to solve this.

Overall, the most efficient way to solve this problem would be to use a combination of a recursive algorithm and mathematical properties to generate and evaluate the minimum number of expressions necessary to find all possible solutions.

ChatGPT loves wrapping up with “Overall,“. I still want my algorithm though.

I pressed it further, asking for specific examples and further explanations, and examples including those explanations. This is where things started to fall apart pretty quickly.

Here it is trying to write a function that outputs every permutation of operations and parentheses, to be done for each permutation of the 4 digit number.

def add_operations_parenthesis(numbers):
    if len(numbers) == 1:
        return numbers[0]
    else:
        expressions = []
        for i in range(1, len(numbers)):
            for operator in ['+', '-', '*', '/']:
                left = add_operations_parenthesis(numbers[:i])
                right = add_operations_parenthesis(numbers[i:])
                expressions.append("(" + left + operator + right + ")")
        return expressions

It seems to have forgotten how the parentheses are supposed to work. It also seems to have forgotten how python works and what equations it’s supposed to generate. This doesn’t even run, and even if it did, the recursion logic is totally borked. That said, I’m still pretty stunned at just how close to a good solution this is, for a robot.

When I (gently¹) brought up how parentheses should work, I got my first (of many) response that opened with “I apologize, you are correct”. If ChatGPT had a catch-phrase, this would be it. Then with all its computational might it came up with this genius fix:

- expressions.append("(" + left + operator + right + ")")
+ expr = "(" + left + operator + right + ")"
+ if expr.count("(") == expr.count(")"):
+     expressions.append(expr)

Its solution is to still generate all the same equations, but now check if there are the same number of '(' as ')'. Which, as a result of the statement immediately preceding it, will always be true. Good grief!

Here it is then sorting each of those equations to somehow filter out duplicates with the associate property. Not even close, pal.

solutions = set()
for permutation in permutations_list:
    permutation_list = list(permutation)
    expressions = add_operations_parenthesis(permutation_list)
    for expression in expressions:
        # add associative property check
        expression = expression.replace("+", " + ").replace("-", " - ").replace("*", " * ").replace("/", " / ")
        # sort the elements of the expression
        expression_list = [x for x in expression.split() if x not in ["(", ")"]]
        expression_list.sort()
        # join the expression back
        new_expression = "".join(expression_list)
        result = ast.literal_eval(new_expression)
        if result == 10:
            solutions.add(new_expression)

While this is indeed a function that will do some things, they are not the right things. This just splits the string into an array, sorts all the characters in the expression, ignoring parentheses. This would never work. For the expression 2+3-1*4, it would try to evaluate *+-1234.

Also, it suggests using ast.literal_eval() instead of eval() for a safer option (in addition to verifying the input elsewhere). These are actually very good recommendations in this case, especially with the garbage strings it’s outputting.

Clever, not smart

At this point it seems that some of these are just limitations of how this model is trained as well as how they are shaping its responses as it gets more use. This model isn’t built for the tasks I’m throwing at it, but you can sense that it wouldn’t take much to get it a lot closer.

It became clear to me that ChatGPT is great at explaining things, but terrible at implementing them.

At least the way the model is currently tuned and outputting responses. Maybe this is intentional during the free research preview, but I’m not so sure.

When given very strict requirements and parameters, it was pretty good at outputting a single function. But you really have to direct it, and spot when it’s leading you down the wrong path altogether. Even with a far more advanced model that is able to parse a larger problem down to its constituent parts, combining and adapting those parts into a cohesive final product is not a simple task. As an example, ChatGPT would constantly remind me the example may not handle edge cases, even when it actually did.

So I decided around this point I should switch tactics and actually try leveraging ChatGPT’s strengths. I started asking it high level questions, having it elaborate on different suggestions and solutions and then asking for an example with a very specific scope. I kept at this for a while, correcting its mistakes, prompting it for more examples and refining its output.

Using this approach, I was able to get some really quality information. It started explaining how I could employ a depth-first search algorithm and how expressions could be parsed for duplicates using the sympy library. Again, the implementations were useless, but once I got an idea of how I could use it I was able to ask it more direct questions.

By the end of it, I had a good grasp of some concepts I would want to employ to write this myself. It had explained a variety of approaches and concepts including backtracking, heuristics, hash sets, pre-generated table look-ups and generating a canonical form for each equation.

Fine, I’ll do it myself

Before diving further, I decided to take a step back and re-examine how I’m going to tackle this. So far, this approach has been how to generate all the possible equations and then filter out equations that are duplicates. This is a more programmatic approach than a logical one. For instance, the parenthesis possibilities are reduced when taking into account the operators used. Example: 1+2+3+4 has no possible parentheses that will affect the result.

By checking which operations appear in what order, I can selectively apply the appropriate parenthesis pattern to each permutation. There are only 5 possible patterns for an equation with 4 terms.

Next, in generating these equations, the same pattern is being generated each time. So instead of calculating all the equations for [1,2,3,4], I just need to generate all the equations for [a,b,c,d] and substitute the values.

Now that I have symbols instead of values, I can actually use sympy to simplify the expressions to their canonical form and add them to a set.

To take things a bit further, I generated equations for duplicate numbers as well. Otherwise, something like [2,2,2,2] would process a lot of duplicate calculations.

I put this altogether and generated a JSON file that could be loaded into a solve function in just about any language. On top of that, you could find solutions for every possible input (10!/(10-4)! = 10*9*8*7 = 5040 total solutions).

I have included the code at the bottom of this post, or you can check out this gist. This is just the equation generator, but I’ve included an example of a solver in python (gist) as well. I really only used the python solver a few times since I ended up taking things a bit further…

Next steps

I set out on this little project to solve a very specific problem: 1 ? 9 ? 9 ? 1 == 10. At multiple points I would be inputting test numbers to make sure everything was working and outputting sane results. I had to make sure I never tried those 4 magic evil numbers, spoiling the entire reason for this whole endeavour. Once I finally had the solver outputting an array of solutions, I simply changed print(solutions) to print(len(solutions)) and got my first (and only) hint: there was, in fact, 1 solution.

As I continued on with the project I would come back and give it another crack until finally something clicked. And then, like a thousand times before, I realized I used one number too many times. Alas, (9+1)/9*9 was no good but I was onto something… 10/9 == 1+1/9. I must be a nerd, because I actually started fist pumping in the air when I figured it out: 9*(1+1/9) == 10. Huzzah!

Did I even need to do… any of this? Who cares, I decided I wasn’t done here. I had a pre-generated list of equations, it seemed trivial to write a solver — why not whip up a quick API? Since I’ve been experimenting with the platform a lot lately, I decided to use Cloudflare’s relatively new Workers, with some help from ChatGPT along the way. Check out Part 2 for that journey where I end up writing my first Rust program — a WebAssembly Cloudflare Worker.

Overall,

This turned out to be a very interesting experiment. ChatGPT proved to be a very useful companion and provided some key information to help me along the way.

I have tried using it to build a few other things, but those were generally pretty basic in terms of logic and functionality. It was interesting to see how it could talk you through different approaches to solving a problem, the pitfalls you may encounter, some best practices along the way — but as soon as you ask it to start combining those pieces into coded examples, it quickly forgets important parts of the overall context.

Its ability to quickly parse information in the context you require is nothing short of incredible. The fact that it can actually produce functional examples — limited in scope though they may be — is still pretty mind-blowing. I found dealing with some of the annoyances like the cut-off responses, servers being occasionally overloaded or losing past conversations pretty easy to forgive when I would remind myself of this. For better or worse, this is here to stay and as these models advance, the way in which we interact with the digital world will shift dramatically.

I came across an interesting thought the other day that definitely resonates with me even more after this little project:

ChatGPT isn’t going to take your job; a developer using ChatGPT might

ChatGPT couldn’t write an algorithm for me, but the resources it did provide were pretty impressive. In part 2 you’ll see how quickly I was able to get up and running in a language I’ve never looked at before. Once you start taking advantage of ChatGPT’s strengths, it’s impossible to deny its utility.

Code:

Equation Generator

gist

import itertools
from sympy import Symbol, parse_expr
import json

op_add = ['+','-']
op_prod = ['*','/']

def generate_operations():
    op_permutations = list()

    # Iterates through all permutations of operations
    # Assigns parenthesis sets if order of operations will be affected
    # see add_parentheses() for different patterns
    for op in itertools.product(op_add + op_prod, repeat=3):
        op_paren = [0] # no parentheses, default case
        if op[0] in op_add:
            if op[2] in op_prod:
                op_paren.append(1)
            if op[1] in op_prod:
                op_paren.append(2)
                if op[2] in op_add:
                    op_paren.append(4)
            elif op[1] in op_add and op[2] in op_prod:
                op_paren.append(3)
        if op[0] in op_prod:
            if op[1] in op_add:
                op_paren.append(3)
                op_paren.append(5)
                if op[2] in op_prod:
                    op_paren.append(1)
            elif op[2] in op_add:
                op_paren.append(4)
                op_paren.append(5)
        
        op_permutations.append((op, op_paren))

    return op_permutations

def add_parentheses(eq_array, paren_set):
    if paren_set == 1:
        # Pattern 1: ( X _ X _ X ) _ X
        return ['('] + eq_array[:5] + [')'] + eq_array[5:]
    elif paren_set == 2:
        # Pattern 2: ( X _ X ) _ X _ X
        return ['('] + eq_array[:3] + [')'] + eq_array[3:]
    elif paren_set == 3:
        # Pattern 3: X _ ( X _ X ) _ X
        return eq_array[:2] + ['('] + eq_array[2:5] + [')'] + eq_array[5:]
    elif paren_set == 4:
        # Pattern 4: X _ X _ ( X _ X )
        return eq_array[:4] + ['('] + eq_array[4:] + [')']
    elif paren_set == 5:
        # Pattern 5: X _ ( X _ X _ X )
        return eq_array[:2] + ['('] + eq_array[2:] + [')']
    return eq_array

def generate_equations(operations, input_vals = ['a','b','c','d']):
    eq_symbols = {
        'a': Symbol('a', positive=True),
        'b': Symbol('b', positive=True),
        'c': Symbol('c', positive=True),
        'd': Symbol('d', positive=True)
        }

    equations = list()
    unique_eqs = set()
    permutations = set()

    # iterate through all permutations of input numbers
    # add every operation set to each permutation
    # iterate over each parenthesis set in op_set[1]
    # parse each equation into sympy expression
    # add expression to set if does not exist
    for p in itertools.permutations(input_vals):
        # avoid duplicates if there are repeated numbers
        if p in permutations:
            continue
        permutations.add(p)

        for op_set in operations:
            eq_iter = itertools.zip_longest(p, op_set[0])
            eq_array = [val for expr in eq_iter for val in expr if val is not None]
            for paren_idx in op_set[1]:
                eq_a = add_parentheses(eq_array, paren_idx)
                eq_str = ''.join(eq_a)
                eq_sym = parse_expr(eq_str, eq_symbols)
                if eq_sym not in unique_eqs:
                    # filter out a few known incorrect equations
                    # e.g. a-a*a-a (-3*a); a/a*a/a (1); a-b/(c-c) (a-b/0)
                    if eq_sym.is_nonpositive or eq_sym.is_integer or eq_sym.is_infinite:
                        continue
                    unique_eqs.add(eq_sym)
                    equations.append(eq_str)
    return equations

def generate_equation_map():
    operations = generate_operations()
    # all possible permutations of 4-digit number
    input_perms = [ ['a','a','a','a'], ['a','a','a','b'], ['a','a','b','b'], ['a','a','b','c'], ['a','b','c','d'] ]
    json_obj = dict()
    for perm in input_perms:
        eq_set = generate_equations(operations, perm)
        eq_key = 'eq_' + ''.join(perm)
        json_obj.update({ eq_key: eq_set })

    f = open('./equation_map.json', 'w')
    json.dump(json_obj, f, separators=(',',':'))
    f.close()

generate_equation_map()

Equation Solver

gist

# quick and dirty solution with *no* input validation
# input_num should be string e.g. "1234"
# target should be desired result - 10 in this case
def solve_problem(input_num, target):
    # generate a pattern and value map
    symbols = ['a','b','c','d']
    dupes = dict()
    for n in input_num:
        if dupes.get(n):
            dupes[n] += 1
        else:
            dupes[n] = 1
    pattern = ''
    val_map = dict()
    for (i, val) in enumerate(sorted(dupes.keys(), key=lambda x: dupes[x], reverse=True)):
        val_map[symbols[i]] = val
        pattern += symbols[i] * dupes[val]

    # load equations from json
    f = open('./equation_map.json',)
    eq_map = json.load(f)
    eq_list = list(eq_map['eq_'+pattern])
    f.close()

    # evaluate each equation
    # check result against `target`
    # return solutions
    solutions = list()
    for eq in eq_list:
        parsed_eq = ''.join(list(map(lambda x: val_map[x] if x in ['a','b','c','d'] and val_map.get(x) else x, eq)))
        try:
            if eval(parsed_eq) == target:
                solutions.append(parsed_eq)
        except(ZeroDivisionError):
            continue
    return solutions